수학: 계산기
기술은 우리의 질문에 빠르고 효율적으로 답해줍니다.
가령, 왜 하늘은 파란가, 내 친구 생일은 언제지, π 값은 얼마인가를 물어볼 수 있습니다.
기술을 사용해서 이런 질문에 대한 답을 받는 것으로는 충분하지 않습니다.
기술의 진짜 강점은 자신이 스스로 만들 수 있는 플랫폼으로 사용할 때 펼쳐집니다.
내가 원하는 기능이 들어간 계산기를 만든다고 합시다.
기본 계산기 안에 넣고 싶은 기능은 무엇인가요?
아래에 적어보세요.
(__)
좋습니다. 이 기능을 추가한다고 합시다.
이 추가 기능을 어린 아이에게 설명한다면 어떻게 설명하시겠습니까?
(__)
수학과 컴퓨터 과학에서는 함수를 일련의 입력 값에 어떤 처리를 한 후 나오는 출력값을 얻는 것으로 정의합니다. 가령, F(X)=X*X 이라면 F(3)=9, F(10)=100 입니다.
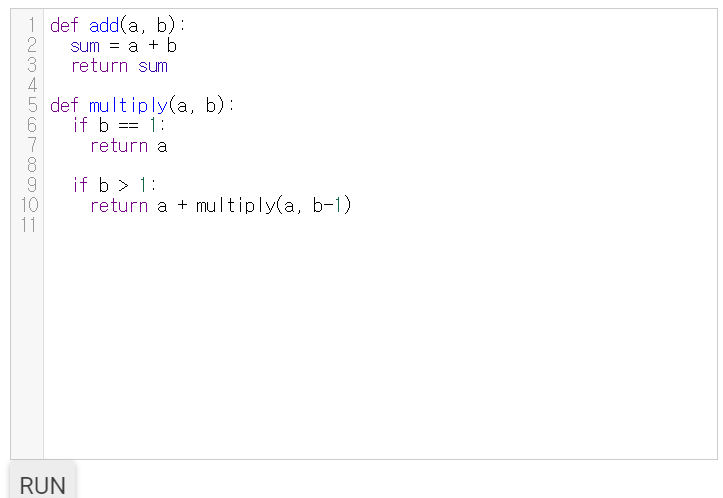
계산기는 add 라는 함수를 만듭니다. 이 함수는 두 개의 입력값을 받아 두 숫자의 합을 출력값으로 만듭니다. 가령, 더하기(3, 5) → 8 이 되죠.
add 알고리즘은 이렇습니다.
입력값에 두 숫자를 넣는다.
두 수를 더한다.
결과를 출력한다.
계속하려면 다음을 클릭하세요.
더하기 알고리즘의 예는 파이썬 프로그래밍 코드에도 있습니다.
코드를 실행한 후, 다양한 입력값을 넣어보세요.
이제 add(a,b) 코드를 볼 때마다 그 결과를 a와 b를 더한 것으로 보세요.
그렇지만 이 활동에서는 +(더하기로 처리)를 사용하기를 써서 더하는 함수를 구현해도 괜찮습니다.
곱셈은 어떨까요? multiply(a,b)라고 하는 함수를 사용하면 됩니다.
그러면 두 입력값을 받아 곱을 한 결과를 보여줍니다.
기존에 있는 덧셈 함수를 사용해서 곰셈 함수를 만들 수 있나요?
다음으로 가시려면 [다음]을 클릭하세요.
계산기에서 곱셈함수를 만드는 한 방법은 재귀를 사용하는 것입니다. 재귀란 수학이나 컴퓨터 과학에서 사용하는 개념입니다. (주: 재귀는 자신을 정의할 때 자기 자신을 재참조하는 방법을 뜻합니다.) 재귀는 자기 자신을 알고리즘에 넣어서 풀 수 있는 작은 문제 단위로 문제를 푸는 형태입니다.
수학에서 재귀의 유명한 예제는 피보나치 수열을 들 수 있습니다. 피보나치 수열은 1, 1, 2, 3, 5, 8, 13, .... 와 같이 다음에 올 숫자는 그 전 두 숫자의 합의로 정의되는 형태입니다. F(n)=F(n-2)+F(n-1)로 말할 수 있습니다. 가령, 1에 1을 더하면 2가 되고, 그 다음 1에 2를 더하면 3이되는 형태로 됩니다. 이 패턴은 곰셈 알고리즘을 개발할 때 유용합니다.
계속하려면 [다음]을 클릭하세요.
add 함수를 사용해서 곱셈 함수를 하는 코드를 살펴봅시다.
과제 : 수 a와 수 b를 곱하기
법칙1 : 만일, b가 1이면, 정답은 a 이다.
법칙2 : a와 b-1를 곱한 결과에 a를 더한다.
예시: 5*4
(5 * 3) + 5
((5 * 2) + 5) + 5
(5 * 1) + 5) + 5 + 5
5 + 5 + 5 + 5
Answer is 20
계속하려면 [다음]을 클릭하세요.
재귀함수에서 "기저사례(base case)"는 필요하다.
왜냐하면 재귀함수가 언제 멈춰야 할지 정해주기 때문이다.
법칙1은 기저사례다. 이유는 곱셈의 항등원이 1이기 때문이다.
이 함수는 b가 1이면 반드시 멈춰야 한다.
앞의 예에서 코드를 다시 재기록했었다.
이 알고리즘에 근거한 자신만의 함수를 다시 적어보자.
과제 : 수 a와 수 b를 곱하기
법칙1 : 만일, b가 1이면, 정답은 a 이다.
법칙2 : a와 b-1를 곱한 결과에 a를 더한다.
add 함수를 사용해서 곰셈함수를 적을 수 있다면, [다음]을 클릭하세요.
곱셈 알고리즘의 예제로 아래 파이썬 코드 프로그래밍을 제시했다.
다양한 입력값을 넣어보며 코드를 [실행]해보자.
(역자 주: 원문에서는 파이선 코드가 나옵니다)
이것은 덧셈함수를 사용해서 곰셈 함수를 만드는 예시다.
만일 재귀함수를 멈추게 하는 법칙1의 기저사례가 없다면 어떤 일이 일어날까? 함수는 절대 멈추지 않을 것이다. 그렇다면 왜 컴퓨터는 이 문제를 확인하지 않을까?
이 문제는 멈춤문제(halting problem)로 알려져 있다. 우리 인간은 진행과정을 보며 끝나려면 시간이 얼마나 걸릴지 알 수 있다. 그러나 컴퓨터는 언제 끝날지 알 수 없다. 따라서 알고리즘을 작성할 때 추가로 주의해야 한다.
계속하려면 [다음]을 클릭하세요.
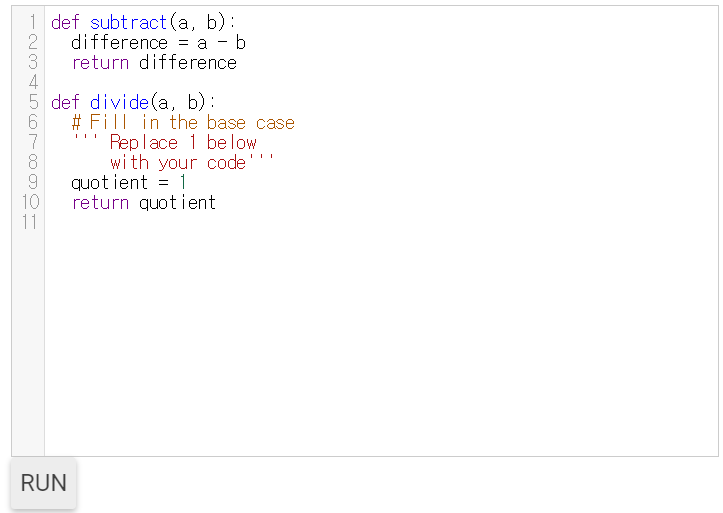
이전 예제에서 완수한 것을 바탕으로
즉 재귀 빼기 함수를 사용하여 다음은 앞의 예에서 수행 한 내용을 바탕으로,
뺄셈함수를 재귀적으로 사용해서 아래 나눗셈 함수의 없어진 부분을 채워봅시다.
재귀는 이해하기 어려운 개념입니다.
따라서 재귀함수 문제를 다룰 때 낙심하지 마세요.
계속해서 코딩해보고, 시각화하며, 시도해 보세요.
지금까지 계산기를 만드는 작업이 잘 진행되고 있습니다.
지금까지는 기본적인 작동방법에 관한 설명이었습니다.
이제 다음 단계로 가서 제곱근함수와 로그함수를 만들어 봅시다.
square(a)→a2 or log(a)→log10a로 표현합니다.
나만의 계산기를 만드는 작업은 우리가 큰 문제를 대할 때,
함수를 사용해 작은 문제들로 나누어 해결하는 컴퓨팅 사고 활동의 좋은 예입니다.
함수를 사용함으로써 작은 문제로 나눠 해결하는 것을
이미 우리는 앞에서 곰셈 알고리즘을 만들 때나 나눗셈알고리즘을 다룰 때 사용했었습니다.
이 주제에 대한 구체적인 설명이 필요하면 재귀와 함수 프로그래밍을 인터넷에서 찾아보세요.
부트스트랩 과정은 프로그램을 통해 학생들에게 대수와 기하학적 개념을 가르칩니다.
이 활동에서 사용 가능한 교육기준도 참고 하세요.
기술을 사용할 수 없는 상황에서 학생들은 알고리즘을 작성할 수 있고,
그것을 알고리즘을 설계하는 사람에게 테스트해주라고 요청할 수 있습니다.
잘했습니다! 아래 버튼을 클릭해서 이 코스를 계속하세요.